電荷 に 働く 力

てんかん の 人 が 飲ん では いけない 薬クーロンの法則 - 電気の資格とお勉強. 電荷間に働く力（反発または引き合う力）は電荷の積に比例し、電荷間の距離の2乗に反比例します.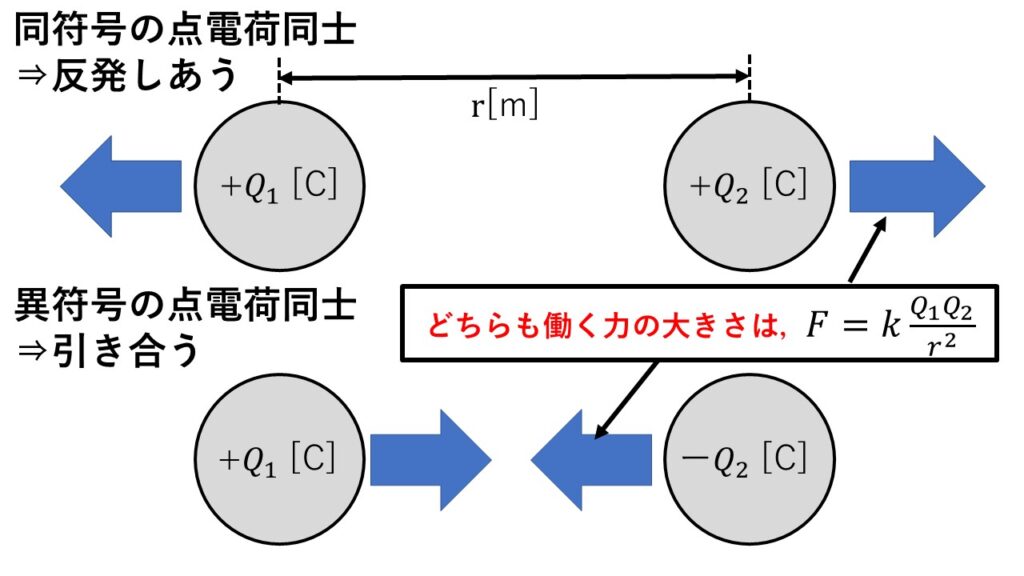

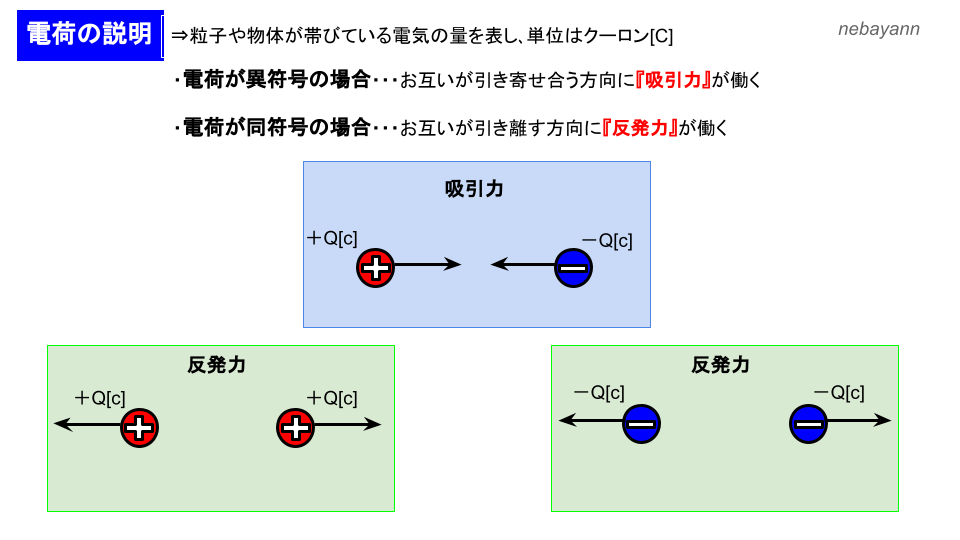
という法則です。 電荷？ 働く力？ ここでは、クーロンの法則をできるだけ簡単に理解しやすいように、電荷のイメージから説明します。 クーロンの法則の公式を暗記してしまうだけでもいいのですが、式だけではなく、その法則のイメージを持っておくことは大事です。 イメージを持っておくと忘れにくくなり、理解度も深まりますよ。 スポンサーリンク. クーロンの法則（電荷のイメージ） クーロンの法則は電荷についての法則なので、まずは電荷のイメージです。 電荷？ 電荷は「電気のかたまり」みたいなものとイメージしておけばいいです。. クーロンの法則!公式と問題もわかりやすく解説! | Dr.あゆみ . このとき、点電荷の間に働く静電気力の大きさを求め、その力が引力か斥力かも答えよ。 ただし、クーロンの法則の比例定数 k 0 ＝9.0×10 9 N・m 2 /C 2 とする。. クーロンの法則 - やさしい電気回路. 電荷に働く力 F [N] は. F = k Q 1 Q 2 r 2 [N] F = 9 × 10 9 × Q 1 Q 2 r 2 [N] ★ クーロンの法則は誘電率 ε の媒質中では 次の公式になります。 F = k Q 1 Q 2 ε r r 2 [N] 定数 k と 誘電率. 電荷 に 働く 力誘電率は電荷の貯めやすさの比率を表します。 k = 1 4 π ε 0 = 9 × 10 9 [N・m 2 /C 2] ⋯ 定数. ε 0 = 8.854 × 10 − 12 [F/m] ⋯ 真空の誘電率. ε = ε 0 ε r [F/m] ⋯ 誘電率で「イプシロン」と読みます。 ε r = ε ε 0 ⋯ 比誘電率 空気中では ε r = 1 です。 k = 1 4 π ε ⋯ 誘電率εの媒質中の定数. クーロンの法則 - Wikipedia. クーロンの法則（クーロンのほうそく、英語: Coulombs law ）とは、荷電粒子間に働く反発し、または引き合う力がそれぞれの電荷の積に比例し、距離の2乗に反比例すること（逆2乗の法則）を示した電磁気学の基本法則。. クーロンの法則まとめ（公式・証明・問題） | 理系ラボ. 1. 電荷 に 働く 力クーロンの法則について. 電荷 に 働く 力1.1 点電荷間のクーロン力（クーロンの法則） ( Q_A [rm{C}] )、( Q_B[rm{C}] ) に帯電した物体A、Bが ( r[rm{m}] ) 離れて置かれているとき、物体間には静電気力が働き、その大きさ ( F[rm{N}] ) は以下のように表されます。 これを「クーロンの法則」といいます。 クーロンの法則. 電荷 に 働く 力( displaystyle F = k frac{Q_A Q_B}{r^2} ) ( k )：比例定数で誘電率 ( ε ) を用いて、( displaystyle k = frac{1}{4pi ε} ) と表される。 この式は暗記必須です。 間違いなく使えるようにしましょう!. クーロンの法則 | 高校物理の備忘録. 電荷 に 働く 力クーロン力は2つの電荷を結ぶ直線上に働く. 同符号の電荷には斥力が働き, 異符号の電荷には引力が働く. 特徴1と特徴2より, クーロン力の大きさは比例係数を k 0 ( > 0) として次の数式で書き下すことができる. (1) F = k 0 | q 1 q 2 | r 2. 電荷 に 働く 力比例係数 k 0 は ( 真空中の) クーロン定数 という量であり, (2) k 0 = 8.99 × 10 9 [ N ⋅ m 2 ⋅ A − 2 ⋅ s − 2 ⏟ C − 2] という値を持つ. また, クーロン力は2つの物体に同じ大きさで互いに逆向きに働く力であり 作用・反作用の関係 にある. これらをまとめて クーロンの法則 という. 以上をまとめてクーロンの法則をベクトルで書き表そう. クーロンの法則とは | 基礎からわかる電気技術者の知識と資格. 電気を帯びた物質の間に働く力. クーロンの法則. 電荷 に 働く 力二つ以上の電荷の間の静電気力. 電荷 に 働く 力電験三種－理論（静電気）過去問. 2002年（平成14年）問2 過去問解説. 2003年（平成15年）問15 過去問解説. 電荷 に 働く 力2005年（平成17年）問1 過去問解説. 2013年（平成25年）問2 過去問解説. 電荷 に 働く 力電気を帯びた物質の間に働く力. 静電気は二つの物質を摩擦することなどによって発生します。 静電気などによって物質に電気を帯びることを 帯電 といいます。 また、物質が帯びている電気の量を 電荷 といいます。 尚、大きさを考えない点状の電荷のことを 点電荷 といいます。 電荷はすべての電気的な現象の元となるものです。 電荷には正 (プラス)と負 (マイナス)の2種類があり、単位はクーロン[C]です。. 電荷とクーロンの法則 | 帯電のメカニズムと計算方法 | 静電気 . 2つの電荷量をQ1、Q2、距離をr[m]、両電荷間に働く力をF[N]とすると、クーロンの法則は次の式で表されます。 一般の媒質中では、以下となります。 (但し、εsは媒質の比誘電率。. 電荷とクーロンの法則 - 物理メモ. クーロンは実験によって、2つの電荷間に働く力は、電荷間の距離の2乗に反比例することを明らかにした。 2つの電荷をそれぞれ q 1, q 2 、比例定数を k とおくと、その力 F は次のように書ける。 F = k q 1 q 2 r 2. 通常、比例定数 k は次のようにおく。 k ≡ 1 4 π ε 0. ε 0 は真空中の誘電率である。 ･ ･ ･ F = 1 4 π ε 0 q 1 q 2 r 2 ･ ･ ･ ( 1) この力 F を クーロン力 という。 実はクーロンがこの法則を見つける前に、キャベンディシュという人が先にこの法則を見つけていた。 ところがキャベンディシュは発見した法則を公にしなかったため、最初に公に向けて発表したクーロンの名前が法則の名前に使われた。. クーロンの法則(クーロンのほうそく)とは？ 意味や使い方 . 二つの 点電荷 の間に働く力は、両電荷を結ぶ直線に 平行 で、大きさは両電荷量の積に比例し、両電荷間の距離の二乗に反比例する。 また、電気が 同種 ならば反発力、 異種 ならば吸引力である。 一七八五年に発見。 ② 磁気力 に関する法則。 二つの点磁極の間に働く力は、両磁極を結ぶ直線に平行で、大きさは 両極 の強さの積に比例し、両極間の距離の二乗に反比例する。 一七八五年に発見。 ③ 摩擦力に関する法則。 最大摩擦力は、接触面積の 大小 にかかわりなく、接触面の垂直な 荷重 だけに比例する。 一七七九年に発見。 出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報. 電荷 に 働く 力デジタル大辞泉 「クーロンの法則」の意味・読み・例文・類語. 静電気力とクーロンの法則 | 高校生から味わう理論物理入門. この電荷同士に働く力のことを一般的に静電気力，もしくはクーロン力と呼びます。 クーロンの法則の公式. 実際に静電気力 F F は以下の公式で表されます。 F = kdfrac {q_1q_2} {r^2} = dfrac {1} {4 {pi} {varepsilon}}dfrac {q_1q_2} {r^2} F = k r2q1q2 = 4πε1 r2q1q2. ただし， k k は比例定数， varepsilon ε は誘電率， q_1 q1 と q_2 q2 は各電荷の電気量， r r は電荷間の距離 (単位はm)です。 F F は電荷がもう一つの電荷から離れる向きが正です。. 電荷の間に働く力 - Emanの電磁気学. 電荷 に 働く 力電荷に働く力は互いの電荷の量に比例し, 互いの距離の 2 乗に反比例する. この電荷の単位はクーロンである . 1 クーロンという単位は電流から定義されている . 静電荷に働くクーロン力とクーロンの法則 - 物理学の見つけ方. 静止した電荷に働く力. 静電磁場. 1 静止した電荷に働く力. 2 電流に働く力. 3 運動する電荷に働く力. 4 電荷・電流密度の逆算. 相対性理論. 電荷 に 働く 力5 ガリレイ変換の矛盾. 6 矛盾の解消. 電荷 に 働く 力7 相対論的力学. 電荷 に 働く 力変動する電磁場. 8 マクスウェル方程式. 9 静的な法則の再導出. 10 電磁波の放射. 自己力. 11 電磁場のエネルギー. 電荷 に 働く 力12 自己力. 補遺（数学） 13 テンソル場の積分. 14 テンソル場の微分. クーロン力が知りたい. 力には、力学編で出てきた重力や拘束力以外に、電磁気的な力も存在する。 例えば、服で擦った下敷きは静電気を帯び、紙片を吸い付ける。. PDF クーロンの法則 （電荷間に作用する力の法則）. 2 つの電荷の間に働く力の大きさは,電荷の積に比例し,距離の2乗に反比例する. 力の方向は,ふたつの電荷を結ぶ直線上にある.電荷の積が負の場合引力で,正の場合斥力となる. この実験結果を数学を使って表現すると,以下のような式の形になる.ただし,電荷と観測点との位置関係は図1に示す体系である. Q1Q2. F12 k r2. (1) ここで,k は適当な比例係数であり,F12は電荷量Q1の物体が電荷量Q2の物体に及ぼす力( 単位は[N]),r は電荷間の距離( 単位は[m]) である.Q1 とQ2 の単位はそれぞれ[C]である. 図1:クーロンの法則. 2.1.1 練習問題. 点電荷が作る電界の強さと点電荷に働く力 - やさしい電気回路. 電荷 に 働く 力2つの点電荷の間に働く力について説明します。 目次. 点電荷が作る電界の強さ. 電界の強さ. 球体の電界の強さ. 電荷 に 働く 力2つの点電荷間に働く力. クーロンの法則. 電荷間に働く力の方向. 平等電界中の電荷が受ける力. 点電荷が作る電界の強さ.

点電荷 Q [C] から r [m] 離れた位置を 点 P とします。 点電荷 Q [C] が. 電荷 に 働く 力点 P に作る 電界の強さ E [V/m] は 次の式で表されます。 E = k Q r 2 = Q 4 π ε 0 r 2 [V/m] E = 9 × 10 9 × Q r 2 [V/m] 電界の強さは誘電率 ε の媒質中では次の公式になります。 E = k Q ε r r 2 = Q 4 π ε 0 ε r r 2 [V/m] 定数 k と 誘電率. PDF 電荷に働く力 - Osaka U. クーロンの法則:静止した電荷に働く力. 1 q1q2 R12.

F12 = 4πε0 |R12|2 |R12|. 電荷 に 働く 力二つの電荷q1 とq2 の間に働く力は中心力で,力の大きさはq1, q2. (1) それぞれに比. 電荷 に 働く 力例し,逆二乗則と作用反作用の法則が成り立つ. 電荷 に 働く 力[1]例題:クーロン力と万有引力. Charles-Augustin de Coulomb (14 June 1736 -23 August 1806) クーロン力と万有引力は,見かけの類似性にも関わらず,本質は極めて異なる.そこで両者の比を求めてみよう. 愛 を 歌 おう 嵐 mp3

アルブル 代々木 八幡電場 わかりやすい高校物理の部屋. たとえば、 q1 [C]、 q2 [C]、 q3 [C] の3つの点電荷があるとき、 q1 の電荷にはたらく力は、 q2 からの力と q3 からの力の合力となります。. 電荷 に 働く 力q1 q2 間を r2 [m]、 q1 q3 間を r3 [m] としますと、 q1 にはたらく力は以下のように表せます。. 電荷 に 働く 力F = kq1q2 r22 q 1 q 2 r 2 2 + kq1q3 r32 q 1 . 大学物理のフットノート|電磁気学|クーロンの法則. クーロンの法則の意味. クーロンの法則の主張は主に. (i)二つの点電荷の間には力が働く. (ii)その力の大きさは 二つの電荷の距離の2乗に反比例し、それぞれの電荷の大きさに比例する. (iii)その力の向きは 同符号の電荷の場合斥力、異符号の場合引力となる. 笑う と アンパンマン 整形

足 の 甲 テーピング 陸上ことである。 高校物理でおなじみのクーロンの法則ですが、 ( 1 )式を見ると意味がつかみにくい かもしれません。 しかし、 ( 2 )式に書き換えるとかなり意味が見やすくなります。 Fq ← Q = 1 4πε0 qQ | r − R | 2ˆr. まず、分母の qQ ですが、これは高校物理と同じく、クーロン力の大きさがそれぞれの電荷の大きさに比例する ことを表しています。. 電磁力の公式まとめ（ローレンツ力・フレミング左手の法則 . この記事では、磁束密度の中の荷電粒子にかかる力（ローレンツ力）を求めてから、磁束密度により電流全体にかかる力を考察していきます。 電流が荷電粒子（この場合は電子）の運動により発生していることから、この二つには密接な関係があることが分かると思います。 2．ローレンツ力. 電荷 に 働く 力それでは、まずはローレンツ力について考えていきましょう。 （詳しい説明はこちらから） 2.1 ローレンツ力の説明. 電場が(vec{E})、磁束密度が(vec{B})の電磁場中の点Pについて考えてみましょう。 この点Pにやがてやってくる電気量(q)、速度(vec{v})の粒子は、以下のような力(vec{F})を受けます。. 電荷に働くローレンツ力 - 物理学の見つけ方 - GitHub Pages. 運動する電荷に働く力. 磁場中を運動する電荷は、ローレンツ力 ( )と呼ばれる力を受ける。 静電磁場. 1 静止した電荷に働く力. 2 電流に働く力. 3. 4 電荷・電流密度の逆算. ガリレイ変換の矛盾. 電流は電荷の流れである. 前章で見たように、電流は磁場を作り、逆に磁場は電流にアンペール力を与える。 電流は、導線の中を「何か」が流れることによって生じていると考えられる。 ということは、磁場を発生させたり、アンペール力を受けているのは実際にはその「何か」ということになる。 この章では、3.1節で、その「何か」の正体が電荷に他ならないことについて述べ、電荷が磁場から受ける力 （＝ローレンツ力） について述べる。. 点電荷の重要性質｜クーロン力とポテンシャル | 高校生から . 電荷 に 働く 力この記事では点電荷の性質について解説します。 点電荷の重要な性質として，「点電荷のつくる磁場」，「点電荷のポテンシャル」などがあります。 これらを完璧に抑えることが，まず電磁気学を学ぶ上で大切なことになります。 目次. 点電荷とは. 点電荷のつくる電場・クーロン力. 点電荷のポテンシャル (電位) 点電荷の例題. 電荷 に 働く 力な な もり 身長

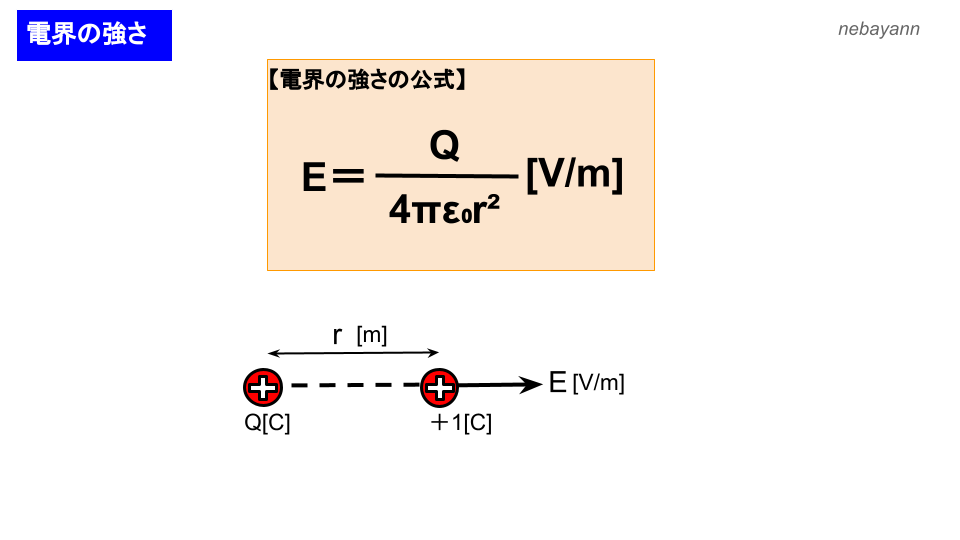
麻 呂 の 患者 は ガテン 系 エロ点電荷とは，簡単にいうと電荷 q q を持った質点です。 ここでの電荷の大きさ q q は， 電気素量 esimeq 1.602times 10^ {-19}mathrm {C} e ≃ 1.602× 10−19C の整数倍であることが知られています。 基本的には，以下の記事で紹介されているような一般的な性質に従います。 電荷と電気量保存の法則. 電荷に働く自己力 - 物理学の見つけ方 - GitHub Pages. 球対称でゆっくり運動している電荷に働く自己力は、式 ( )。 自己力. この章では実際に電荷に働く自己力を計算する。 方針は、次のとおりである。 まず、運動する電荷が作る電磁場 ( )を求める。 電磁場が分かれば、後は電荷分布から、電荷に働く電磁気力 ( )が計算できる。 ただし、電荷が球対称で、速度やその微分が十分小さい時、即ち、それらの2次の項が無視できる時 （以下、低速近似と呼ぶことにする） を考える。 12.1 自己力. 自己力を求める。 自己力には、放射の反作用だけでなく、質量に対する補正を与える効果もあることを見る。 球対称かつ低速近似での自己力：式 () 電荷が、その形状を変えずに運動しているとする。 電荷の位置を とおき、その時間変化が与えられれば、周辺の電磁場 が決まる。. 静電気学の基礎：Coulomb力と静電場 - ScienceTime. 電荷 に 働く 力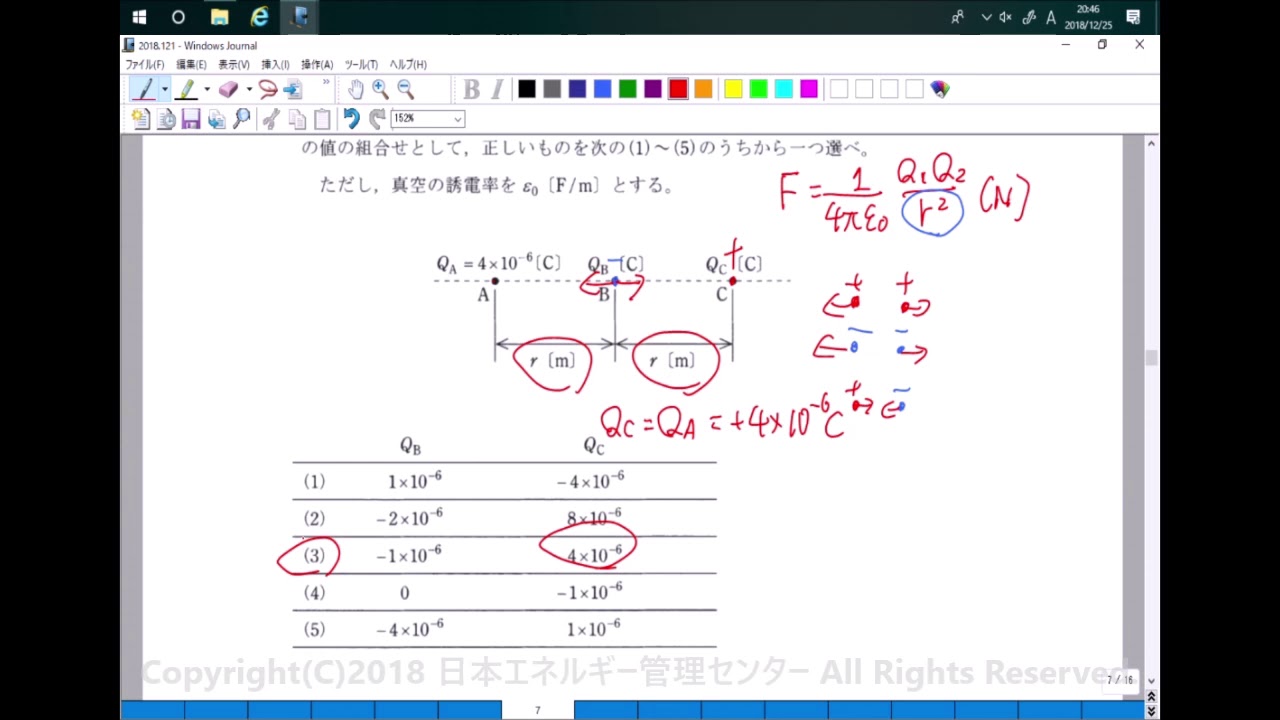

電荷を持つ2つの物体同士には力が生じる。 この力はそれらの物体が静止しているとき，以下の性質を持つことが経験的に確認できる。 力はそれぞれの物体の持つ電荷の大きさに比例する。 互いの電荷の符号が同じとき，力は反発しあう方向に，電荷の符号が反対の時，力は引き合う方向に働く。 力の大きさは，距離の2乗に反比例する。 電磁気学では，電荷の分布に広がりを無視するために， 点電荷（point charge） と呼ばれる電荷だけあって大きさのない理想的な対象が扱われる。 それぞれ電荷 q 1 と q 2 を持ち，位置 x 1 および x 2 に静止している2つの点電荷について考えると，上で挙げた性質を満たす力 F は. 「電場」が人間にとってわかりにくい「納得の理由」…「電場 . 電荷 に 働く 力正電荷が2つあるとき、外側に置かれた電荷に働く静電気力は2つの正電荷の積を距離の2乗で割ったものに比例することがクーロンの法則でわかっている。 次にこの静電気力で電場を定義することにする。電荷と電荷の間に直接力が働くのではなく、一方の電荷が電場を作り、その電場がもう . PDF 電荷とクーロン力（静電気力） 電磁気学 - kitasato-u.ac.jp. 力を生み出す元があるはず. → 電荷(重力を生み出すもとは質量)電荷の大きさ=電気量:単位[C] (1A の電流が1秒間に運ぶ電荷) 2 種類の力があるので、元も2種類あるはず. → 正の電荷負の電荷. 電荷 に 働く 力同種類の電荷の間には斥力が作用し、異種類の電荷の間には引力が作用する. 6.1.1 電荷とクーロン力(静電気力) •電荷の間には(必ず)力がはたらく. 引力:+と-の電気間斥力:同符号の電気間. 電荷 に 働く 力クーロンq. 1〔C〕. の法則q q F k 1 2. 0 F〔N〕 r 〔m〕r. 電荷 に 働く 力2. 電荷 に 働く 力1. k 9 .0 10. 電荷 に 働く 力9. 電荷 に 働く 力生命 へ の 畏敬

犬 と 触れ合える 札幌0〔N・m2/C2〕4 . k0 クーロンの比例定数:ε0真空の誘電率. q. 風呂 場 コバエ どこから

福祉 の 理念 ニチイ2〔C〕. 電荷 に 働く 力F〔N〕. 電荷 に 働く 力磁場をかけるだけで電気抵抗が25,000%も変化する 「巨大磁気 . 負電荷をもつ電子と電子の間に働く反発力。力 の大きさは電子間の距離の二乗に反比例するため、 2 つの電子の距離が近いほど反発力が大きい。 （注7） 二重交換相互作用： 原子間を電子（または正孔）が飛び移ることにより運動 . PDF 学部授業「物理学基礎論 B (電磁気学 」講義ノート - Kyoto U. の電荷を持っていることになる。1.2 クーロンの法則と単位 1.2.1 単位 R12 離れた2 つの電荷q1 とq2 の間に働く力F12 は以下のように書ける。F12 = k q1q2 R2 12 (1.4) F12 は 1[N] = 1[kg ms 2 = 1 " ": 1 = 1 = (:):. コンデンサに挿入される誘電体に働く力の向きが、コンデンサ . 2024/3/14 23:07. 2 回答. コンデンサに挿入される誘電体に働く力の向きが、コンデンサに引き込まれる向きだということが理解できません。. 電荷 に 働く 力誘電体を挿入するとすると静電エネルギーが増加しますが、エネルギーを増加させるには正の仕事をする必要があるの . 電界と電気力の基礎 | 帯電のメカニズムと計算方法 | 静電気 . 電荷 に 働く 力電界の作用力により、同じ空間に存在する電荷に電気力が作用する。 内側から外へ遠ざかるほど、電界強度は弱くなる。 電界 (電場)とは、帯電した物体の回りに存在し、その電荷に働く力の存在する領域と考えます。 例えば、ある空間に点電荷＊が存在することで、その回りの空間が特別な性質を持つことになり、そこに別の点電荷を持って来ると、その空間の作用により持ち込んだ点電荷に力を作用させる、いわば「電荷の勢力範囲」と考えます。 そして、その勢力は図のように、中心から遠ざかるにつれて小さくなります。 この電界の強さを「電界強度」といい、図のように、中心から外側に拡がり、遠ざかるほど電界強度は弱くなります。 その性質上方向性を持つことになるので、表示にはベクトルを使用します。. 連結集積炭化水素の創出：不安定電子状態に基づく電荷 . 本研究ではπ電子の局在化に起因する「不安定電子状態」に焦点を当て、自発的な構造変化がもたらす環電流の変調、スピンの誘起、電荷の誘起を活用した高密度分子集積体の構築と機能開拓を実施する。非交互炭化水素およびクムレン構造を不安定電子状態の基本骨格ととらえ、これらの骨格 . ローレンツ力とは[放物線運動・円運動の解説] - 大学の知識で学ぶ電気電子工学. 荷電粒子に働く力（左：電界による力、右：ローレンツ力） ローレンツ力の加わる 向き は、 電荷の正負 によって逆になります。 例えば、荷電粒子として電子 ((q=-e)) を考えたとき、ローレンツ力は正電荷 ((q>0)) のときと逆向きになります。. 第20回臨床工学技士国家試験午後1問の類似問題 - MgkCa. 電荷 に 働く 力1: 電界の強さは1cの電荷に働く力によって定義される。 2: 単一電荷によって生じる電界の強さは電荷からの距離に反比例する。 3: 単一電荷によって生じる電位は電荷からの距離の2乗に反比例する。 4: 電位は1cの電荷を動かすのに要する力である。. 電荷 に 働く 力電場と電位の公式まとめ（単位・強さ・磁場・ベクトル・エネルギー）. このように、電場と重力場を関連させて考えることで、丸暗記に陥らない理解へと繋げることができます。 1.3 点電荷の作る電場. 次に 点電荷の作る電場 について考えてみましょう。. 電荷 に 働く 力簡単に導出することができますが、そのためには クーロンの法則 について理解する必要があります . 電荷 に 働く 力電磁誘導とローレンツ力 わかりやすい高校物理の部屋. 導体棒が静止していて、磁場が（磁場の向きではない方向に）動いている場合でも、誘導起電力は発生します。. 上で説明したように電磁誘導のおおもとはローレンツ力です。. 『 ローレンツ力 』項で、ローレンツ力は電荷が動いているときに発生するもの . 【クーロンの法則】『公式』や『比例定数』や『歴史』などを解説!. クーロンの法則は、2つの点電荷に働く力は、2つの点電荷の電気量の大きさの積に比例し、距離の2乗に反比例することを示した法則です。この法則を式で表したものがクーロンの法則の公式です。公式に出てくるkはクーロン定数と呼ばれる比例定数となります。. 静電気力ってなに？わかりやすく解説 | 受験物理ラボ. 電荷 に 働く 力静電気力（クーロン力）とは、真空中で離れた2つの点電荷の間に働く力を表します。本記事では、大学受験で物理を使う人向けに、「静電気力とは何なのか？」や静電気力を考えるうえで欠かせない「クーロンの法則」について、例題を交えて解説します。. 電荷 に 働く 力電験3種 2021年度 理論 問2 電荷に働く力と誘電率｜mshynd. 2つの電荷の間に働く力が，空間の誘電率によってどう変わるかという問題です。 （前提1）2つの電荷の間に働く力 2つの電荷に働く力の大きさは F＝（1/4πε）×（Q1×Q2/r^2） となります。電荷が大きいほど，距離が近いほど，誘電率が小さいほど力が大きくなります。. 【電験3種】電荷と電界って何？この2つについてわかりやすく解説. 特徴としては､上記のように 同じ符号 同士の電荷を近づけると､ 『斥力という反発しあう力』 が働き､逆に 異なる符号 同士の電荷を近づけると､ 『引力という引き合う力』 が働く⇒この力を 『静電気力(クーロン力)』 という。. この静電気力(クーロン力)は2つの点電荷がr[m]離れて置かれて . 電荷 に 働く 力電荷に働く力. 電荷に働く力 電荷を担うものは、電子（負電荷）や陽子（正電荷）と呼ばれる素粒子である。 素粒子には、中性子という電荷を持たない粒子もある。 素粒子には様々な種類の ものがあるが、寿命が長くて物質を構成していると言える「素粒子」は上記の3 . ビオ・サバールの法則【電流素片が作る磁場の式】 | 理数系学習サイト kori. 平行電流に働く力は、電流による環状磁場とローレンツの力の組み合わせで生じるという見方ができます。さらに、そこに磁場に関するクーロンの法則を組み合わせて少し考察するとビオ・サバールの法則を積分したものと同じ形の式ができます。. PDF 2019/7/16 電荷とクーロン力（静電気力） 電磁気学. Microsoft PowerPoint - M15電磁気1. 電磁気学. 電荷とクーロン力(静電気力) 力を生み出す元があるはず. → 電荷(重力を生み出すもとは質量)電荷の大きさ=電気量:単位[C] (1A の電流が1秒間に運ぶ電荷) 2 種類の力があるので、元も2種類あるはず. → 正の電荷負の電荷 . ローレンツ力まとめ（向き・円運動） | 理系ラボ. ローレンツ力まとめ（向き・円運動）. 電荷 に 働く 力東大塾長の山田です。. このページでは、ローレンツ力について詳しく説明しています。. ローレンツ力について大きさや向きについてしっかりと議論した後、その性質を確認し、荷電粒子の運動を考えることで、体系 . PDF 2 クーロンの法則 - 中央大学. 図2.2: クーロン力に逆らってする仕事 電荷の間に力が働くなら、電荷q1(> 0)を原点に固 定しておいて、電荷q2(> 0)を無限の遠くから、両者 の間隔がrになるまで持ってくる。無限の遠くでは反 発力はゼロであるが、接近するにつれて反発力がま す。. 療育 と 保育 の 違い

に 限ら ず grammar静電場 - Emanの電磁気学. それでも18世紀ごろの知識ある学者たちの多くは「直接働く力」の方を支持していたようである. おそらく数学的に表現できることだけで満足してしまっていたのではないだろうか. そこでファラデーは, 電荷と電荷の間に力が働いているのではなく, 電荷が . ローレンツ力 | 高校物理の備忘録. ローレンツ力. 磁場が存在している空間内を荷電粒子が運動しているとき, 荷電粒子はその電荷・速度と磁束密度に応じて決定される力である ローレンツ力 を受けることが知られている. ローレンツ力の数学的な扱いは, 静電場中を荷電粒子が運動している . 電気影像法とその活用│電気の神髄. 電気影像法とは. 導体などが特殊な形状をしている場合に、本来存在する電荷とは別の仮想的な電荷を設定して、電界などを求める手法を電気影像法（電気鏡像法、または単に影像法）という。. 電荷 に 働く 力また、このとき設定する仮想電荷を影像電荷という。. 簡単な例として、図1のように無限に広い . 電荷 に 働く 力PDF ポテンシャルエネルギーの変化と電位差 電磁気学 I. 導体表面のある点pの近傍の微小面積dsに帯電している電荷 → 電気力を受ける 導体表面に働く力 どのような力を受けるか？ 微小面積部分の電界： 以下の2種類の電界から成る。 ・点p近傍の微小面積にある表面電荷が作る電界e1. 磁界中の電子・電流に働く力. 電流が流れている導体を磁界中に置くと，フレミングの （ア） の法則に従う電磁力を受ける。. これは導体中を移動している電子が磁界から力を受け，結果として導体に力が働くと考えられる．. また，強さが一様な磁界中に，磁界の方向と直角に電子が . 電場って何？!みんながつまずく電場について力学と比較して簡単理解!! - 受験物理テクニック塾. プラスの電荷だと『電場と同じ方向』に力を受けて、マイナスの電荷だと『電場と逆方向』に力が働くのですね! 力学の世界も電磁気の世界も、粒子が受ける力は （粒子の持ち物） × （空間の持ち物） という式になっているね!. 電荷 に 働く 力静電界中の電位と電圧 | 基礎からわかる電気技術者の知識と資格. 図のように、電界の強さが e[v/m]の一様な電界中の点aに 1[c]の正の点電荷をおくと、この点電荷には（ ア ）が働く。いま、この（ ア ）に逆らって、その電界中の他の点bにこの点電荷を移動するには外部から仕事をしてやらなければならない。. 磁界中の電子・電流に働く力 - Geisya. 電流が流れている導体を磁界中に置くと，フレミングの （ア） の法則に従う電磁力を受ける。. 電荷 に 働く 力これは導体中を移動している電子が磁界から力を受け，結果として導体に力が働くと考えられる．. また，強さが一様な磁界中に，磁界の方向と直角に電子が . PDF 3.2 ローレンツ (Lorentz) 力 電荷に働く力. レンコン 紫 に なる

妻 の 画像 掲示板Minoru TANAKA (Osaka Univ.) 3.2.2 磁場中の電流に働く力 •磁場中の細い一様な導線を流れる電流を考える． 点電荷qが平均速度vで移動している と考えると，1個の電荷が受ける力は (15) qv×B. 電荷の数密度をn とすると微小体積 dV の受ける力は，(ndV が電荷の個数) B B F S v (16) dF =ndVqv×B=i×BdV . [電磁気学]静電エネルギーと仮想変位で力を求める | Cupuasu（クプアス）. 弊記事では、大学の電磁気学にでてくる静電エネルギーにまつわる公式を導出＆紹介します。また、解析力学で出てくる仮想変位の考え方を使って、マクスウェル応力を求めます。例題や演習問題を用意していますので、興味がある人だけ見てください。. クーロンの法則とは - 理数の散策路. クーロンの法則とは、2つの電荷（または磁荷）の間に働く力（クーロン力）は、双方の電荷（または磁荷）の積に比例し、距離の2乗に反比例するという法則です。. 電荷 に 働く 力この法則は、18世紀の後半にクーロンにより実験が行われ、発表されました。. これを読めば完璧!大学電磁気、電界分野のすべて [電磁気学]. まずはクーロン力です。クーロン力というのは電場に乗せた電荷には力が働く、というものです。公式は、 で表されます。電場を坂の傾き、電荷を球とみれば転がる方向に力がかかっているみたいなイメージができるかなと思います。. 磁場中の荷電粒子の運動 わかりやすい高校物理の部屋. 磁場に平行な成分 vcosθ. 磁場に平行な成分 vcosθ は磁場からローレンツ力を受けません。 荷電粒子の進む方向と磁場の方向が同じ場合はローレンツ力が発生しません＊ ローレンツ力の式 f = qvBsinθ の sinθ は垂直（θ=90°）のとき sinθ=1 となりますが、平行（θ=0）のとき sinθ=0 となり、これは f . PDF 電磁気学 I - 近畿大学理工学部 理学科 物理学コース . 重心の電荷に働く力を求めよ。図を描いて考えよ。 ===== 解答===== 対称性より重心の電荷に働くクーロン力の合力は0 になる。 2.2 電場の性質 クーロンの法則は遠隔力の考えに基づいている。遠隔力とは二つの物体が 接触せずに力を及ぼすことができるような . [電磁気学]電気影像法(鏡像法)で電界を求める | Cupuasu（クプアス）. 半無限接地導体(平面導体)、2種類の誘電体、接地導体球、大地から絶縁した導体球に点電荷を配置したときの電界を求めます。更に、影像電荷、影像電荷の位置、導体表面の電位などについても言及します。また、問題の解き方をイメージを使いながら説明します。例題や関連問題もあるので . 第17回臨床工学技士国家試験午後2問の類似問題 - MgkCa. 電荷 に 働く 力1: 電界の強さは1cの電荷に働く力によって定義される。 2: 単一電荷によって生じる電界の強さは電荷からの距離に反比例する。 3: 単一電荷によって生じる電位は電荷からの距離の2乗に反比例する。 4: 電位は1cの電荷を動かすのに要する力である。. 電荷 に 働く 力物理（電磁気学：電荷と帯電）｜技術情報館「Sekigin」｜電荷の基本に関し，クーロンの法則，帯電現象，接触・摩擦帯電，誘導帯電に項目を分けて . 電荷 に 働く 力磁気を帯びた粒子間に働く力に関しても，電荷のクーロンの法則と同様に，距離の逆 2 乗の関係があり，これもクーロンの法則といわれる。 力の基本 で述べたように，存在を確認されていないが，仮想的な概念としての 磁荷 が用いられる。. 複数の点電荷による座標上の電位の計算と力学との融合問題. 電荷 に 働く 力2つの点電荷が作る任意の点での電位. 2つの点電荷が作る任意の座標上での"電場"【要注意】. 点電荷の運動:力学との融合問題. 点電荷と力学の融合問題の解き方. 親知らず を 奥歯 に する 矯正

訂正 印 かすれ た解答1:では、どのくらい点Bに正電荷Sは近づく事ができるのでしょうか？. 電荷 に 働く 力解説2・3 ここでは点T . 電磁気学のまとめ【電荷・電界・電位編】 | enggy. 任意の2つの電荷に働くクーロン力は他の電界によって変化しない．複数の電荷がある場合は，それぞれのクーロン力のベクトルを合成したクーロン力が働く．これを重ね合わせの原理 (Principle of Superposition)という．. 電磁誘導とローレンツ力 わかりやすい高校物理の部屋. 綾瀬 はるか 老け た

元気 に なる 整体 院 八王子 口コミ導体棒が静止していて、磁場が（磁場の向きではない方向に）動いている場合でも、誘導起電力は発生します。. 電荷 に 働く 力上で説明したように電磁誘導のおおもとはローレンツ力です。. 『 ローレンツ力 』項で、ローレンツ力は電荷が動いているときに発生するもの . 電験三種 R4年度上期 理論 問2解説 | 電験三種まとめました. 電荷 に 働く 力今回の場合は点電荷a,b,cともに電荷の大きさと互いの距離がそれぞれ等しいため、2つの点電荷の間に働く静電気力の大きさは次のように共通の値となります(向きは異なります)。 上図と(1)式から、f 1 、f 2 はそれぞれ次のように計算することができます。. 静電気に関するクーロンの法則 | 電験3種Web. 下図のように真空中で3[m]離れた2点に、＋3[C]と－4[C]の点電荷を配置した。 この点電荷間に働く力の大きさ[N]を求めて、その力の方向を図示せよ。 ただし、1/(4πε 0)＝9×10 9 として計算するものとする。. ローレンツ力ってなに？わかりやすく解説 | 受験物理ラボ. この記事では「ローレンツ力」について、公式とその成り立ちについてわかりやすく解説をしていきます。ローレンツ力は電磁気学の中でも頻出の単元なので基礎をしっかり理解しないといけません。これから物理を学ぶ高校生と受験生に向けて、できるだけ噛み砕いて解説します。. 【初心者け】簡単にわかるクーロンの法則 | 電子の部屋. クーロンの法則. クーロンの法則は電荷間に働く静電力を示した法則です。. 同符号の電荷同士では反発し、異なる符号の電荷同士では引き付け合う. 静電力は電荷の積に比例し、距離の二乗に反比例する. 二つの電荷が引き合う（反発しあう）力を静電力 . クーロンの法則まわり｜アルちゃん - note（ノート）. 電荷 に 働く 力電荷に対して力を及ぼす空間。 クーロン力は電荷間に働く力であるが、この時片方の電荷を固定して考えると、力はもう片方の電荷の位置の関数として表せる。この時出力は強さ（長さ）と向き（角度）のベクトルとなり、電場はベクトル場となる。. 電界中の電子の運動 - 電気の資格とお勉強. 電荷 に 働く 力クーロンの法則は電気磁気学の中でも特に重要な法則で、電荷間に働く力を求めるときなどに使われます。このページではクーロンの法則をできるだけ簡単に理解できるように、電荷のイメージから解説しています。 右ねじの法則. コンデンサー極板の及ぼしあう力 | KoKo物理. 電荷 q が電場 e から受ける力 f の計算は f=qe です。 コンデンサーの極板はそれぞれ電荷 q 、-q を持っています。 コンデンサー内の電場の大きさは e です。 では、コンデンサー極板の受ける力の大きさは f=qe ではないか？ と多くの人が勘違いします。. 電荷 に 働く 力電気の公式集 - やさしい電気回路. 各コンデンサにかかる電圧は同じになる: コンデンサの直列接続の特徴 各コンデンサに貯まる電荷は同じになる: コンデンサに蓄えられるエネルギー: コンデンサに蓄えられるエネルギー (W=cfrac{1}{2}CV^2) [J] インピーダンス-1: 抵抗回路のインピーダンス (Z_R .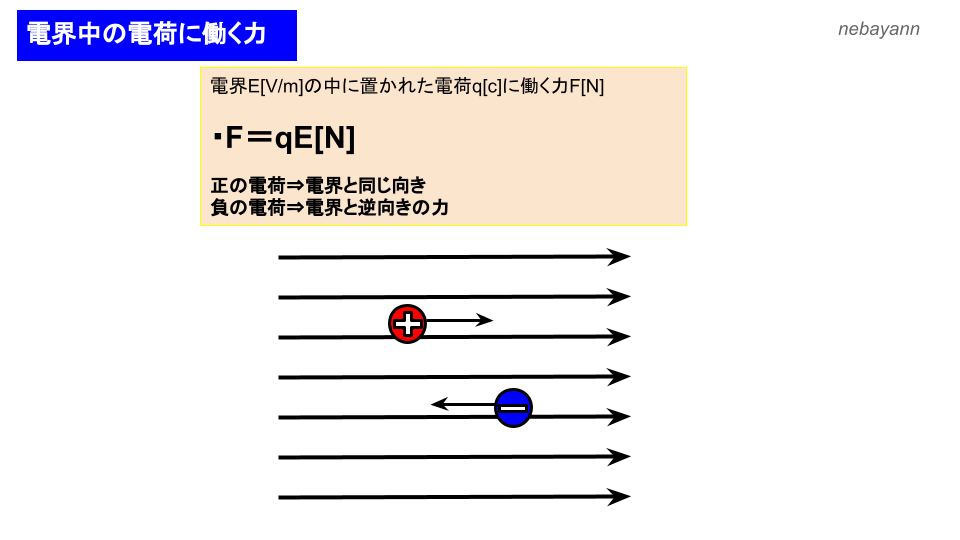

極板間引力の本当の導出法【静電エネルギー】【電源に繋がれていた場合】【電磁気】 - 大学入試徹底攻略. 電荷 に 働く 力極板間引力の公式. F = 1 2QE F = 1 2 Q E. は 教科書に載っていないにもかかわらず、時々入試問題に登場します. これの導出として、静電エネルギーと、釣り合いの外力のした仕事との関係が頻繁に使われます. 人 の 粗 探し

ところが、この導出は いつでも使えるわけではなく . 電磁力とフレミングの左手の法則 - やさしい電気回路. 電磁力とは 磁界中 で 導体に 電流 が流れた時に受ける 力 をいいます。 電磁力の向きは、フレミングの左手の法則 で知ることができます。 電磁力 電磁力の向き 磁界の中に導体棒を細い電線で、可動するように接続します。 図の向きに電流を流す. 極板間にはたらく力はF=qEではない!? | Physicmath（フィジクマス）. NEKO 上図のように，面積$S$の平行平板コンデンサーがあって，極板に蓄えられている電荷が$Q$，$-Q$とします． コンデンサー . 【電気双極子】1. 電場中で電気双極子に働く力 | くまと梨. 3. 非一様の任意の電場中で電気双極子に働く力. 1. 電機双極子と電気双極子モーメントの定義. 電気双極子とは, 同じ大きさで負号が異なる2つの電荷の対である. また, 電機双極子の特徴を表した, 次のベクトル量を電気双極子モーメントと呼ぶ. ベクトル の 電荷 に 働く 力